【実生活の中の受験勉強vol.1】電気料金と一次関数

学校の勉強なんてやる意味あるの？将来役に立つの？
誰もが一度も疑問に思ったことがあると思います。
役に立つとか立たないとかそういう問題じゃない！とかいろいろ意見はありますが、
ココではひとまず、実生活の中で見つけたものを紹介します！

電気の契約を見直したい！

たしかに今の電気会社B社では基本料がかかっています。基本料無料なのは魅力的に見えますが、
実際お得なんでしょうか？
計算して確かめてみましょう！

電気料金の計算方法

電気の契約は、多くの場合 基本料 ＋ 従量課金 となります。
基本料とは、電気をどれだけ使おうと毎月定額でかかる料金、
従量課金とは、その月電気を使った量に応じて加算される料金です。

つまり、
毎月の料金1000円 ＋ 今月は100kWh使ったので2000円
＝ 3000円
のように計算されます。

条件の整理

もう少し細かい料金の設定を比較してみると、次の通り。

B社がなかなか複雑で難しそうですが、一つ一つ整理していきましょう！

実際に計算してみよう

先月の使用料での比較

先月の私の電気使用量は 101kWh でした。これでまずは計算してみましょう。

A社 : 101kWh × 26.4 ≒ 2666円
B社 : 101 × 20.85 + 1144 ≒ 3250円

ということで、先月の使用量ならA社のほうが安いことがわかりました。

使用量が変動したらどうなる？

先月の使用量101kWhではA社のほうが安いことがわかりましたが、電気の使用量は毎月一定ではありません。
他の値でも調べてみましょう。

50kWhの場合
A社 : 1320円 B社 : 2187円
120kWhの場合
A社 : 3168円 B社 : 3646円

どうやら、使用量が変動してもA社のほうが安そうです。

一次関数の利用

一次関数とは？

いくつかの値を例にして調べてみましたが、すべての値を調べていては非効率的です。
そこで役に立つのが、 一次関数 の考え方です。

いったんおさらいしておきましょう。

どうでしょうか、不安があったら復習してみてくださいね。

グラフを描いてみる①

実際に今回の問題を立式してみましょう。

A社
1kWhあたり26.4円
→ y = 26.4x

B社
基本料1144円、1kWhあたり20.85円
→ y = 20.85x + 1144

電力使用量を変数 x (kWh) とおき、1kWhごとの料金を係数に、基本料を定数項と置けば立式できますね。

これをグラフにすると、以下のようになります。

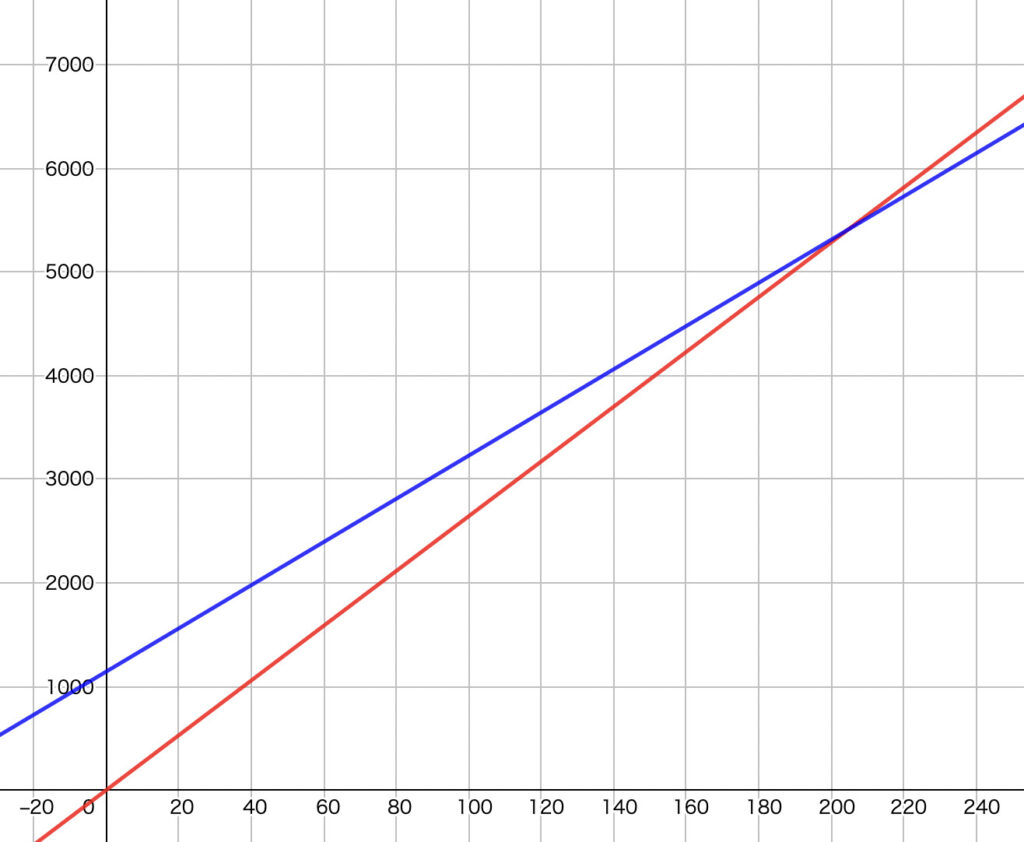
交点のx座標は、A社とB社の式を連立して
26.4x = 20.85x + 1144
5.55x = 1144
x ≒ 206.1 kWh

ということで、206kWh以下ではA社のほうが安く、206kWhを超えるとB社のほうが安いということになりました。

定義域

ところで、B社の料金は使用量によって1kWhあたりの料金も変化する仕組みでした。

1kWhあたり20.85円という料金設定は120kWhなので、
先ほどの

y = 20.85x + 1144

という式が適用されるのは、使用量が120kWhまでの場合ということになります。
つまり、xは0から120の間となり、数学的には以下のように表記します。

y = 20.85x + 1144 （0 ≦ x ≦120）…①

この、「xは0から120の間」という範囲を 定義域 と呼びます。
定義域と似た用語に「値域」というものもあります。あやふやな人はしっかり復習してくださいね。

これを踏まえて、120kWh以上の部分もグラフを描いてみましょう！

グラフを描いてみる②

120〜300kWhの部分のグラフはどうなるでしょうか？

まず、１kWhあたり24.77円なので、係数は24.77

y = 24.77x + b （120 < x ≦ 300）

となりますが、問題は定数bです。

電気料金は、例えば150kWh使用した場合、120kWh分は①の式、そして120kWhを超えた30kWh分を１kWhあたり24.77円で計算します。

例:150kWhの場合
20.85 × 120 + 24.77 × 30 +1144
≒ 4389 円

ということは、
120kWh（3646円）から1kWhあたり24.77円で加算されるという仕組みです。
グラフに表してみると以下のようになります。

では、この120〜300kWh部分（破線部分）の式を求めてみましょう。

条件を整理すると
・1kWhあたり24.77円かかるので、この直線は傾き24.77である。
・点P (120 , 3646) を通る

求める直線を
y = 24.77x + b とおき、
これが(120,3646)を通る、即ち代入すると成立するはずであるから、
3646 = 24.77 × 120 + b
b = 673.6

従って、求める直線の式は
y = 24.77x + 673.6 (120 < x ≦ 300) …②

300kWHを超える分についても求めてグラフにしてみましょう。
同様の方法でできますので、ぜひ自分で求めてみて下さい！

これで必要な式が出揃ったので、今度こそA社とB者の電気料金をグラフにして比較してみましょう。

A社
y = 26.4x

B社
① y = 20.85x + 1144 (0 ≦ x ≦120)
② y = 24.77x + 673.6 (120 < x ≦ 300)
③ y = 26.49x + 157.6 (300 < x)

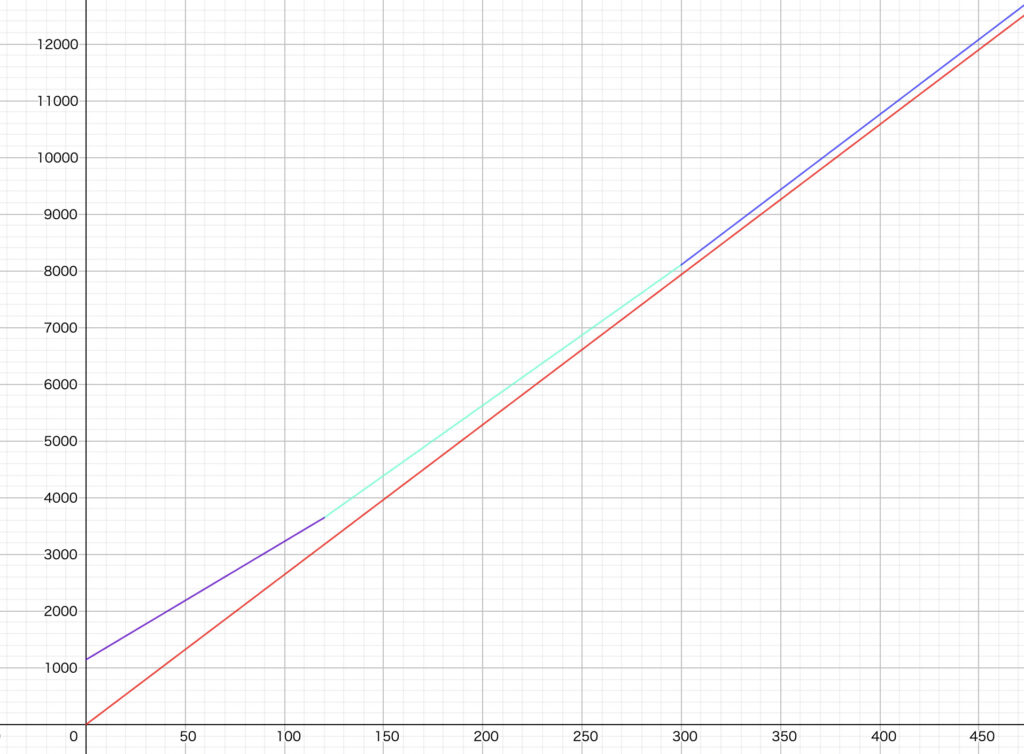
グラフを描いてみると、A社のほうが安いことが一目瞭然ですね！
（A社は傾き26.4、B社の③が傾き26.49とB社のほうが傾きが急なので、
このグラフの外側でもA社がずっと安いことがわかります。）

まとめ

今回の例以外にも、ガス代や携帯料金など、この考え方は生活の中の様々なものに利用できます。
また、基本料＋従量課金という形のもの以外にも、契約金や初期費用などがかかるものに対して、何ヶ月以上契約すれば安くなるかといった計算も同様に行うことができます。

センター試験から共通テストに変わり、卑近な話題を題材にした問題が出題されるようになり、実際にある予備校の共通テスト型の模試は同じようにガス代金を題材にした問題が出題されました。

みなさんも、ぜひ学校で習った内容が日常生活でどう活かせるのか、考えてみてくださいね。

余談

A社の値上がり

実際にこの計算をして、A社で契約をしようとしたのですが、ここ最近の原油価格上昇による燃料価格高騰の煽りを受け、A社の料金が値上がりするとの説明がありました。具体的には1kWhあたり30円程度になるとの事。

ということで1kWhあたり30円（y=30x）でグラフを描き直してみました。

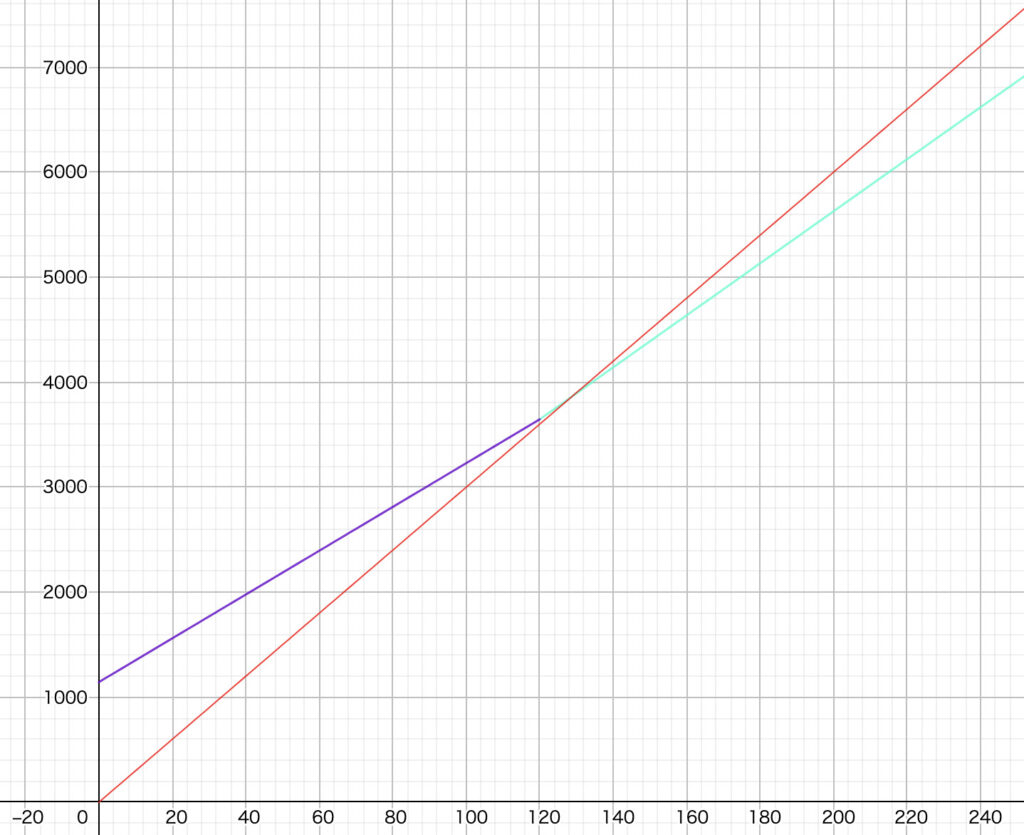
グラフより、交点は② の
y = 24.77x + 673.6 (120 < x ≦ 300)
上にある。
②とy=30xを連立して
30x = 24.77x + 673.6
5.23x = 673.6
x ≒ 128.8

129kWh以上だとB社のほうが安いというなんとも微妙な結果に。
なお、A社が1kWhあたり28、29、31円の時を考えると、それぞれ209kWh、160kWh、113kWhを超えるとB社のほうが安いという結果になりました。

かなり微妙な差かつB社にも当然値上げの可能性があるので、一旦正確な金額が各社から発表されるまで契約は待とうと思います。